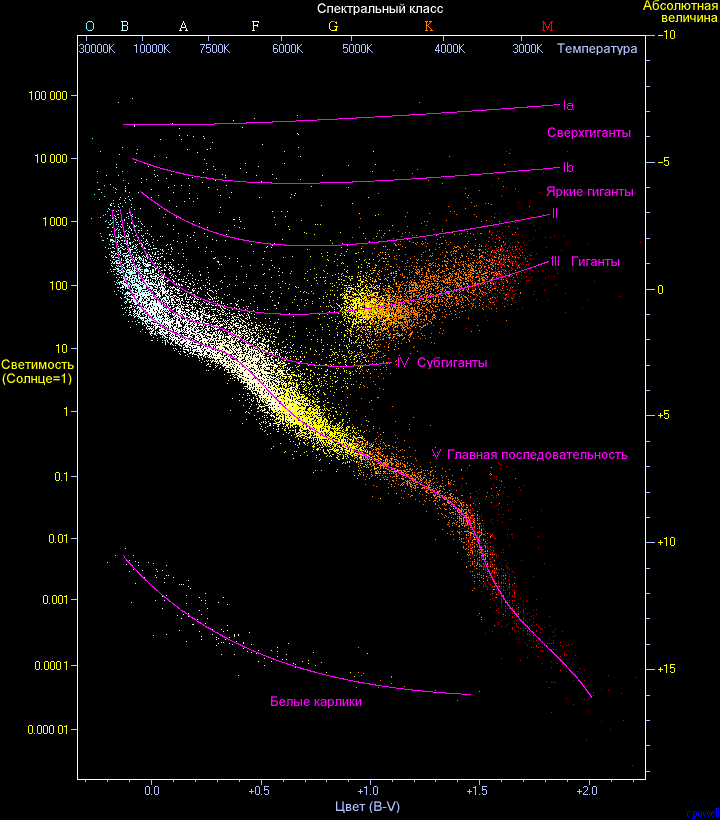
Что такое главная последовательность
В 1905 г. датский астроном Эйнар Герцшпрунг сделал важный шаг вперед: он впервые сопоставил особенности спектров звезд с их светимостью. Выяснилось, что звезды поздних классов (от О до М) резко разделяются на две группы: с очень большой и очень малой светимостью. Герцшпрунг назвал их гигантами и карликами. Действительно, поскольку температура у всех звезд одного и того же спектрального класса одинакова, полная светимость звезды зависит только от ее размеров. Проведенные, начиная с 1919г., прямые измерения диаметров звезд с помощью интерферометра Майкельсона подтвердили, что звезды-гигангы действительно во много раз больше Солнца, и дали хорошее согласие с определениями размеров звезд по их светимостям.
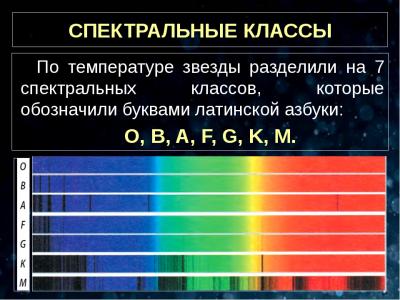
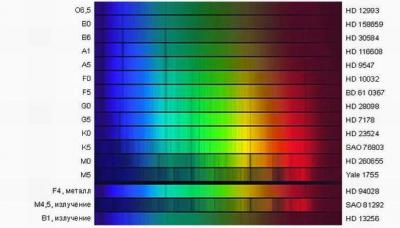
Что касается с-звезд мисс Мори, то они оказались еще больше обычных гигантов. Их назвали сверхгигантами.
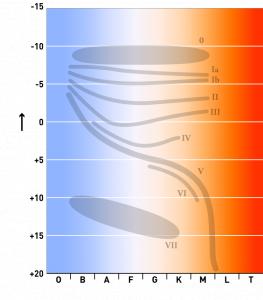
Через несколько лет после Г'ерцшпрупга к изучению связи между спектрами и светимостью звезд обратился уже известный нам Генри Норрис Рессел, построивший в 1913 г. стройную диаграмму «спектр—светимость», которую называют также диаграммой Герцншрунга — Рессела или Г — Р - диаграммой. По вертикальной шкале в ней отложены логарифмы светимости, а по горизонтальной —спектральные классы. Светимость Солнца принята за единицу.
Тут сразу же выявилась интересная особенность этой диаграммы. Звезды не заполняли ее равномерно — они располагались двумя расходившимися ветвями. Одна из них, к которой принадлежало большинство звезд, шла по диагонали вниз и вправо; другая шла почти горизонтально слева направо и состояла из звезд-гигантов. Первая получила название «главная последовательность», вторая — «ветвь гигантов». Солнце, принадлежащее к спектральному классу G и имеющее светимость 1, находилось почти точно в середине главной последовательности.
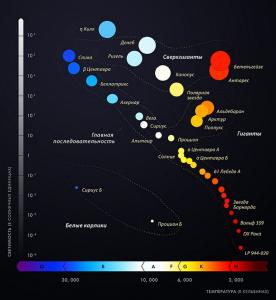
После того как Рессел построил в 1913 г. свою диаграмму, стало возможно связать интенсивность и ширину линий в звездных спектрах со светимостью звезд. Метод такого количественного сопоставления разработали астрономы американской обсерватории Маунт Вилсон, У. Адамс и Кольиноттер. В 1914—1918 гг. они, опираясь на звезды, светимости которых были определены по известным расстояниям и видимому блеску, обратили задачу и стали определять светимости звезд по интенсивности некоторых характерных спектральных линий. Зная же светимость и видимый блеск звезды, можно было определить расстояние до нее. Возможности звездной астрономии сразу расширились — новый метод позволял измерять расстояния до 1300 световых лет, тогда как до этого старым методом годичных параллаксов, верно служившим астрономам 80 лет, можно было мерить расстояния, не превышавшие 300 световых лет.
Получив в руки новое оружие для исследования физических свойств звезд, астрономы немедленно широко им воспользовались. В 20-х годах было завершено в основном построение теории звездных атмосфер. Стало ясно, почему отличаются ширина и интенсивность спектральных линий у гигантов и карликов, несмотря на одинаковую температуру. Гиганты оказались намного разреженнее, чем карлики. Плотности звезд-гигантов оказались в сотни и тысячи раз меньше, чем у Солнца, а у сверхгигантов — в сотни тысяч раз. Поведение спектральных линий зависит от состояния атомов, а последнее — от температуры и плотности газа. При низкой плотности облегчаются процессы возбуждения и ионизации атомов. Вот почему у звезд-сверхгигантов так выделялись с-линии искрового спектра.
Но почему звезды располагались на диаграмме Герц- шпрунга — Рессела неслучайным образом? Видимо, в этом заключался какой-то смысл. Было ясно, что такое расположение звезд как-то связано с их эволюцией. Но как? Что представляла собой главная последовательность, к которой принадлежало наше Солнце?
Звездные модели
Чтобы представить себе, как развивается звезда, надо было знать, как она устроена. Наблюдения давали нам радиус, массу, среднюю плотность звезды и температуру на поверхности. Но как изменяются плотность и температура с глубиной по мере перехода от поверхности звезды к ее недрам? Ясно, что они должны расти, но по каким законам? И как переносится тепло внутри звезды: излучением или конвекцией? Эти вопросы тоже требовали ответа. И ученые давно уже пытались найти этот ответ.
Вернемся опять на полстолетия назад, все к тому же 1862 году. Пока Анджело Секки прилаживал свой спектроскоп к телескопу Ватиканской обсерватории, в далекой Англии Уильям Томсон (Кельвин), изучая термодинамику земной атмосферы, ввел понятие конвективного равновесия. Это был первый краеугольный камень, заложенный в теорию внутреннего строения звезд.
«Всякую сплошную среду, — писал Кельвин, — подверженную влиянию гравитации, будем называть находящейся в конвективном равновесии, если плотность и температура распределены по всей среде таким образом, что поверхности равной плотности и равной температуры остаются неизменными» в случае действия на среду малых возмущений.
Сущность конвективного равновесия, поясняет далее Кельвин, состоит в следующем. Выделим в газовой среде какой-нибудь малый объем и изолируем его от теплообмена с окружающей средой. Если наш объем, расширяясь или сжимаясь, достигнет плотности среды, какую она имеет в некоторой другой точке, то и температура его будет равна температуре среды в этой точке. При этом соотношения между давлением p, плотностью ρ и температурой T будут выглядеть так:
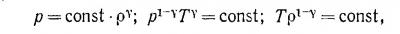
где γ = cp/cv — отношение удельных теплоемкостей при постоянном давлении и постоянном объеме. Изменения состояния газа, подчиняющиеся этим соотношениям, называются адиабатическими и характерны тем, что изучаемый нами объем газа не получает и не отдает тепла (dQ = 0).
Но, как показал Кельвин, можно обобщить эти соотношения на случай наличия притока или оттока тепла, лишь бы величина этого притока была пропорциональна изменению температуры (dQ = cdT). Правда, в этом случае вместо γ = cp/cv надо взять
γ' = (ср — c)/(cv — с).
Изменения состояния газа, описываемые такими обобщенными соотношениями, носят название политропических. Адиабатические процессы — частный случай политропических при с=0.
Соотношение между давлением и плотностью в политропическом процессе можно выразить и так:
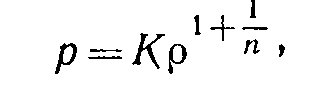
причем величина n носит название показателя политропы. Она играет важную роль в теории конвективного равновесия. Для земной атмосферы n = 5/2.
Выводя уравнение адиабатического и политропического равновесия, Кельвин еще не предполагал, что его можно применить для изучения внутреннего строения Солнца и звезд. Это сделал спустя восемь лет американский физик Гомер Лейн. Любопытно заглавие его работы (1870 г.): «О теоретической температуре Солнца при гипотезе газовой массы, сохраняющей свой объем при помощи внутреннего тепла и зависящей от газовых законов, известных из земных экспериментов».
Сначала Лейн интересовался лишь температурой поверхности Солнца, которая тогда еще не была известна. Как определить ее, зная количество лучистой энергии, испускаемой с единицы поверхности Солнца? «По закону Стефана — Больцмана», — скажет теперь любой студент. Но Лейну этот закон тоже был неизвестен: лишь через 10 лет Стефан нашел его эмпирически и через 15 лет Больцман дал ему теоретическое объяснение. Лейн вынужден был использовать данные экспериментов по излучению энергии нагретыми поверхностями и проэкстраполировать их в сторону больших энергий излучения. Неудивительно, что он допустил довольно большую ошибку: температуру поверхности Солнца он оцепил в 30000°, в пять раз больше, чем в действительности.
Следующей задачей, которую поставил и решил Лейн, было определение плотности солнечного вещества у поверхности. Для этого он должен был рассмотреть равновесие Солнца как целого. Вот тут и пригодились условия конвективного равновесия, введенные Кельвином. Используя их и доказав, что в недрах Солнца молекулы должны раздробиться на атомы в ходе взаимных «жестоких столкновений», Лейн нашел, что показатель политропы солнечного вещества должен равняться 3/2. Затем он решил задачу равновесия газового шара, находящегося под действием собственного гравитационного поля и подчиняющегося политропическому закону
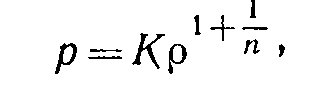
Распределение температуры с расстоянием от центра Солнца выразилось довольно сложным дифференциальным уравнением (его потом стали называть уравнением Лейна — Эмдена), которое решалось до конца только при n = 0, п = 1 и п = 5. Для п = 3/2 решить уравнение точно не удавалось (и не удалось до сих пор), поэтому Лейн применил испытанный приближенный метод: разложил функцию, выражающую зависимость температуры от относительною расстояния, в ряд по степеням этого расстояния, а потом вычислил ее значения для заданных расстояний. Эту функцию Кельвин назвал «функцией Гомера Лейна», а впоследствии она получила название функции Лейна — Эмдена. (Читатель, конечно, заметил, что уже второй раз к фамилии Лейна мы присоединяем фамилию некоего Эмдена. С этим ученым мы скоро познакомимся, а пока пусть читатель не сомневается, что эту честь он вполне заслужил.)
Итак, распределение температуры Солнца с глубиной было построено. После этого не составляло труда, используя политропические соотношения, найти распределение плотности и давления. Плотность вещества Солнца у поверхности получилась у Лейна 0,00036 г/см3. Это примерно в 2000 раз больше современного значения, но не надо забывать, что Лейн принимал температуру поверхности Солнца в 30000°, а такого значения температура Солнца достигает на глубине в 4000 км. Если сравнивать результат Лейна с плотностью Солнца на этом уровне, то окажется, что он ошибся лишь в 20 раз.
Несмотря на эту ошибку, работа Лейна явилась замечательным достижением. Он стал, как отмечает известный индийский астрофизик С. Чандрасекар, не только первым исследователем физических условий в атмосфере Солнца, но и первым исследователем звездных недр, хотя сперва эта проблема его не интересовала.
С именем Лейна связана одна очень важная теорема. Она позволяет от значений функции Лейна — Эмдена для данного относительного расстояния от центра газового шара перейти к значению этой функции для любого другого расстояния. Это — очень удобный закон подобия для распределения температуры, плотности и давления в звездах. И если звезда (или вообще газовый шар) расширяется или сжимается так, что все ее части изменяют свои размеры в одном и том же отношении (такое расширение — сжатие называется однородным), то, согласно теореме Лейна, температура, плотность и давление в каждой точке изменяются обратно пропорционально первой, третьей и четвертой степени этого отношения соответственно. Таким образом, теорема Лейна позволяла рассчитать изменение состояния звезды при ее расширении или сжатии.
Любопытна история этой теоремы. В его работе никаких явных указаний на эту теорему нет. Но когда работой Лейна заинтересовался американский астроном Саймон Ныоком, Лейн сообщил ему об этой теореме и даже дал краткое и простое доказательство. Когда в 1876 г. в Америку приехал Томсон (Кельвин), Ньюком рассказал ему о теореме Лейна и попытался воспроизвести доказательство, но позабыл его. Встретившись после этого с Лейном, Ньюком попросил его написать доказательство специально для Кельвина и вскоре отправил его английскому физику. Кельвин сразу же оценил значение теоремы и впоследствии опубликовал ее, но это было уже в 1887 г.
Между тем в конце 70־х годов проблемой равновесия звезд заинтересовался немецкий физик А. Риттер. За шесть лет (1878—1883) он опубликовал в одном и том же журнале («Wiedemann Annalen») 18 коротких сообщений, в которых, совершенно независимо от Лейна (с работами которого он не был знаком), он выводил закон Лейна и вычислял функцию Лейна — Эмдена для различных значений показателя политропы. Но Риттер пошел дальше и вывел уравнения для внутренней и потенциальной энергии звезды, впервые рассмотрел вопрос о пульсациях газового шара и доказал, что период этих пульсаций обратно пропорционален квадратному корню из плотности звезды. Риттер нашел и условие, отделяющее устойчивые конфигурации звезд (γ > 4/3) от неустойчивых (γ < 4/3). В двух последних своих работах Риттер впервые попробовал рассмотреть теорию звездной эволюции для звезд различной массы (по современной терминологии — для гигантов и карликов), и здесь он высказал пророческую идею о том, что наибольшая светимость, какой может достигнуть звезда, зависит от ее массы.
Но дальше исследование этой проблемы замедлилось. За 35 лет, последовавших после опубликования работы Лейна, за исключением 18 статей Риттера, в печати появилось лишь 10 работ, в той или иной степени дополнявших и развивавших результаты Лейна и Риттера.
Десять работ за треть века! Сейчас ежегодно только по проблеме внутреннего строения звезд публикуется свыше 300 работ. Темпы развития науки стали в наше время иными, отражая общее ускорение развития всего человечества.
Но шестьдесят пять лет назад ученые не спешили. Наступил 1907 год, и вышла в свет одиннадцатая работа по этой проблеме. Но тут мы должны сделать небольшое отступление.
23 августа 1960 г. Американское астрономическое общество организовало в Мексико-Сити (США) специальную лекцию, посвященную памяти Генри Норриса Рессела, скончавшегося за три года до этого. На трибуну поднялся невысокий человек с постоянной улыбкой на лице и заговорил:
«Я начну с краткого экскурса в историю, рассказав о моем дяде».
Те, кто не знал докладчика и его родословную, могли удивиться такому вступлению. Но докладчик продолжал, и вскоре все стало на свои места.
«Мой дядя Роберт Эмдеп написал в 1907 г. книгу, которая была первым фундаментальным трудом по внутреннему строению звезд. В этой книге он использовал рабочую гипотезу, что в любой звезде конвекция является единственным механизмом, переносящим на поверхность энергию, выделяющуюся в глубоких внутренних слоях. На основании этой рабочей гипотезы он построил свое знаменитое семейство политропных моделей».
Так вот кто такой был Роберт Эмден. Его книга «Газовые шары» составила эпоху в истории изучения звездных конфигураций. В ней Эмден не только систематизировал результаты предыдущих исследований (в том числе Лейна и Риттера), но и получил ряд новых результатов, а кроме того, дал таблицы нужных функций. Главная заслуга Эмде- па состояла в строго систематическом исследовании общих решений уравнений конвективного равновесия звезды.
Но вернемся к лекции в Мексико-Сити. Рассказав о заслугах своего дяди, Роберта Эмдена, лектор... Но пришла пора представить вам и самого лектора: американский астрофизик Мартин Шварцшильд, крупнейший современный специалист в области теории внутреннего строения звезд, пионер исследований небесных светил с помощью приборов, установленных на стратостатах. Выходец из Германии, он был вправе гордиться не только своим дядей, но и своим отцом. Отец его, Карл Шварцшильд, был весьма разносторонним ученым: одновременно и прекрасный наблюдатель, и выдающийся теоретик, занимался и физикой звезд, и проблемой строения звездных систем. И в своей ресселовской лекции сын не забыл упомянуть об отце, тем более что это было как нельзя кстати.
«Примерно в то же время, — продолжал М. Шварцшильд, — мой отец обнаружил, что при высоких температурах внутри звезд необычайно эффективным механизмом переноса энергии от внутренних слоев к наружным может быть также излучение. В связи с этим он развил представление о лучистом равновесии и применил его к атмосферным слоям Солнца. При этом он показал, что атмосфера Солнца находится скорее в лучистом, чем в конвективном равновесии. Он нашел также общий критерий, позволяющий установить, находится ли данный слой звезды в конвективном или в лучистом состоянии. Наконец, он предположил, что при переходе к более глубоким слоям под атмосферой мы покидаем слои, находящиеся в лучистом равновесии, и переходим в конвективную зону».
Эта работа Карла Шварцшильда, опубликованная в 1900 г., сыграла важную роль в разработке теории лучистого переноса энергии, теории строения звездных атмосфер и, как мы смогли убедиться, теории внутреннего строения звезд. Итак, вещество звезды могло находиться либо в лучистом, либо в конвективном равновесии. Что такое конвективное равновесие, мы знаем. Надо сказать несколько слов и о лучистом равновесии.
Представим себе некоторый элементарный объем внутри звезды. С одной стороны, он будет непрерывно поглощать часть энергии излучения, приходящего извне через ограничивающую его поверхность. С другой стороны, объем сам будет излучать. Условие лучистого равновесия заключается в том, что количество энергии излучения, поглощаемой объемом, равно количеству энергии, испускаемой нм. Если это условие выполняется в данной зоне звезды, можно утверждать, что эта зона находится в состоянии лучистого равновесия.
Прошло целых 20 лет после опубликования работ К. Шварцщильда и Р. Эмдена, и Артур Эддингтон написал вторую фундаментальную монографию о внутреннем строении звезд. Но вот что интересно: если Эмден строил свои модели целиком на основе теории конвективного равновесия, а К. Шварцшильд допускал двуслойное состояние звезды с переходом от лучистой оболочки к конвективной зоне, то Эддингтон предположил, что во всех звездах от центра до поверхности царит лучистое равновесие и никакой конвекции нет.
В этом вопросе требовалось разобраться. Нужно было провести детальное рассмотрение вопроса о соотношении между лучистым и конвективным переносом энергии. Несколько ученых (А. Уизольд, Л. Бирман, Т. Каулинг), начиная с 1930 г., посвятили этому вопросу свои исследования. Шло последнее десятилетие перед открытием подлинного источника энергии Солнца и звезд. Но астрофизики не ждали, пока это открытие будет преподнесено им на золотом блюде.
Прежде всего, надо ясно представить себе, что в нагретом до нескольких тысяч градусов газе лучистый перенос тепла будет обязательно, а конвекция может возникнуть лишь при определенных условиях. Такие условия наступят, если градиент температуры (скорость ее изменения с высотой) окажется больше, чем при адиабатическом равновесии. В этом случае нагретый объем газа, поднимаясь вверх, не успевает охладиться до температуры внешней среды и стремится подняться еще выше. Возникшие вертикальные токи газа не затухают, а, наоборот, непрерывно поддерживаются. Градиент температуры в ходе конвекции несколько снижается, но остается чуть выше адиабатического.
Немецкий астрофизик А. Унзольд в 1930 г. отметил, что ионизация водорода уже на небольших глубинах (где температура достигает 10000°) порождает мощную конвекцию
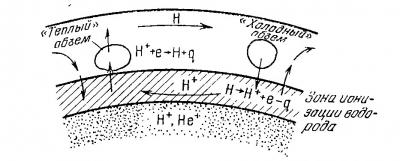
Зона ионизации водорода и конвекция в звезде.
Действительно, с подъемом некоторого объема газа, содержащего ионизованный водород, в нем начинается рекомбинация ионов водорода с электронами — процесс, сопровождающийся выделением тепла (q). Это тепло задерживает охлаждение газа до температуры внешней среды, и объем будет продолжать подниматься. В опускающемся объеме, наоборот, начнется ионизация водорода, требующая затраты тепла, объем не сможет разогреться до «наружной» температуры и будет продолжать опускаться. Унзольд, как за четверть века до него К. Шварцшильд, связал конвекцию в подповерхностных слоях Солнца с хорошо известным явлением грануляции. Но Карл Шварцшильд не мог еще учесть и оценить значение ионизации водорода.
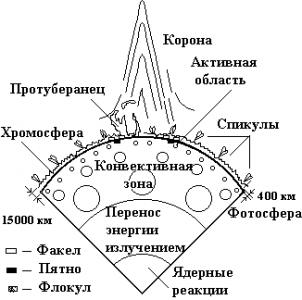
В 1935 г. другой немецкий астрофизик, Л. Бирман, применив к анализу конвекции в звездных недрах метод, развитый гидродинамиком Прандтлем, показал, что глубина конвективной зоны может быть гораздо больше, чем принимал Унзольд, и измеряться десятками тысяч километров. Тремя годами ранее Бирман установил, что в звезде с сильной концентрацией источников энергии к центру должно образоваться конвективное ядро, потому что один лучистый перенос не будет успевать «откачивать» энергию, вырабатываемую в этом ядре чересчур мощными источниками. На основе идей Бирмана англичанин Т. Каулинг разработал ставшую хорошо известной модель звезды с конвективным ядром и оболочкой, находящейся в лучистом равновесии.
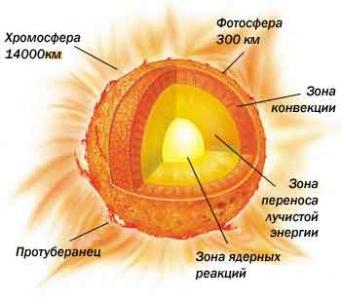
Источники звездной энергии были все еще неизвестны, но их мощность и распределение по глубине использовались астрофизиками для расчета моделей звезд.
Таково было положение на этом участке общего фронта наступления на проблему.
Обратимся теперь к другому участку — к проблеме звездной эволюции. И снова отступим по шкале времени на полвека назад. Отступим назад — чтобы двинуться вперед.
Продолжение следует
Бронштэн В.А. Гипотезы о звездах и Вселенной
|





